There are several Kinematic formalisms that describe the rotational anisotropy of the Universe. That the universe is isotropic, which with homogeneity comprises the Cosmological principle, was viewed as the natural extension to the Copernican principle. In truth it renders Einstein's field equations as analytically solvable.
The following article, entitled the Anisotropic Distribution of High Velocity Galaxies in the Local Group
 https://arxiv.org/abs/1701.06559
https://arxiv.org/abs/1701.06559
highlights the potential problems with the Cosmological Principle assumption of isotropy, a problem for the standard Cold Dark Matter theory based on (a symmetric connection) GR which is highlighted in CMBR surveys
caltech link
https://ned.ipac.caltech.edu/level5/Sept05/Gawiser2/Gawiser3.html
A summary of the observational status is presented in the following article "How Isotropic is the Universe?" published on September 22, 2016 in Physical Review Letters,
https://arxiv.org/pdf/1605.07178v2.pdfg
With this observational motivation to hand it is interesting to consider as the authors do in this article
http://www.mdpi.com/1099-4300/14/5/958 the transition from early to late epoch universe: one initially dominated by spinning matter contributions to Torsion then latterly those non symmetric space-time connection contributions that come from the orbital angular momentum of the aggregate rotation of (the super clusters the make up the large scale structure of the ) the universe as whole.
In light of this we should reflect on the most appropriate kinematical objects and formalisms that should be deployed to describe such asymmetry.
EC represents a minimal extension of GR from which one can encapsulate any violation of the cosmological isotropy principle through a rotating Universe. Once such bulk rotation on aggregate is plausibly identified one must find a means for capturing the universes' inherently orientable character. By enlarging the means by which space-time can be connected and thus its set of invariance preserving co-ordinate transformations, spin and orbital angular momenta contributions from matter can be coupled to the asymmetric ("axial") torsion connection components resulting from a minimally extended Variational Principle.
Orbital Angular Momentum is a Poincare (Lorentzian cross translational) invariant in the purely kinematical arena of Special Relativity in which no dynamics is afforded to its inert (literally!) spatial substrate. Angular momentum is the archetypal pseudo vector as described by axb below.
 In the matter encapsulating, more corporeal accepting General Relativistic dynamical arena it only retains a pseudo-tensorial (density) status. Space-time's malleability in the presence of matter (adhering to either Bose or more pertinently here Fermi statistics) invites orient-ability as well as the curvedness embodied in its holonomy. How do we build on the abstract notion of a rubber sheet manifold?
In the matter encapsulating, more corporeal accepting General Relativistic dynamical arena it only retains a pseudo-tensorial (density) status. Space-time's malleability in the presence of matter (adhering to either Bose or more pertinently here Fermi statistics) invites orient-ability as well as the curvedness embodied in its holonomy. How do we build on the abstract notion of a rubber sheet manifold?
We look to add minimal set of structures to our abstract descriptive space:
https://www.mathphysicsbook.com/mathematics/topological-spaces/generalizing-surfaces/summary/
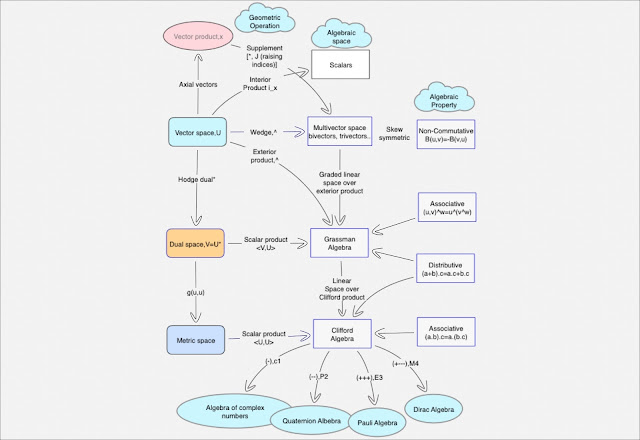
By adding metric structure lengths can be measured and compared at different points in the space if the space does not possess any strange shearing structures. Kinematically the most natural objects to represent spinning matter's frame dragging effects are two spinor-differential (multivector)-forms. Just as half-spin matter fields are most naturally modelled as invariants under the Special Linear Group, (the double cover of the Lorentz group) source term, the tangent space of space-time also affords a natural two-spinor character.

Roughly, while vector objects when parallel transported once around locally flat infinitesimal parallelogram circuits return with same orientation spinorial objects require two circuits in order to return with an identical configuration.
In the language of multi-vectors an orientated parallel-piped volume is equivalent to a pseudo-tensor density with a leading determinant of the space time metric term.
https://en.wikipedia.org/wiki/Multivector
We can see that the "2-blade", 2 forms as an anti-symmetric of one forms defines an orientation. These two planes can be treated as one of the variables in a Variational principle. That is, instead of the (metric/verbein) and connection form we use these bi-vectors as fundamental spatial elements.
Invoking liberally the language of quantum theory, in such schema the irreducible parts of fermionic matter and bosonic space-time both share a common spinor structure.
Pseudo-vectors such as the archetype angular momentum vector are most naturally described by the (Hodge) dual of a multi-form. This is because in the multi-vector formalism, the dual object is intrinsic to the space. That is, no higher-dimensional reference space need be invoked to encapsulate an otherwise extrinsically defined orientation-inducing action of identifying an axis of rotation.

Duality in the sense can operate on the locally flat tangent space indices (of the verbein) as well as on the generalised co-ordinate space.
Using the former Hodge "star" facilitates the construction of both self-dual Curvature (of the connection) objects and self-dual two-forms of orientated 2-spaces (of parallelograms, say). Lagrangians that deploy these most natural Chiral 2-forms are de-facto oriented formulations of gravity.
http://www.mdpi.com/1099-4300/14/5/958
The following article, entitled the Anisotropic Distribution of High Velocity Galaxies in the Local Group
 https://arxiv.org/abs/1701.06559
https://arxiv.org/abs/1701.06559highlights the potential problems with the Cosmological Principle assumption of isotropy, a problem for the standard Cold Dark Matter theory based on (a symmetric connection) GR which is highlighted in CMBR surveys
caltech link
https://ned.ipac.caltech.edu/level5/Sept05/Gawiser2/Gawiser3.html
A summary of the observational status is presented in the following article "How Isotropic is the Universe?" published on September 22, 2016 in Physical Review Letters,
https://arxiv.org/pdf/1605.07178v2.pdfg
With this observational motivation to hand it is interesting to consider as the authors do in this article
http://www.mdpi.com/1099-4300/14/5/958 the transition from early to late epoch universe: one initially dominated by spinning matter contributions to Torsion then latterly those non symmetric space-time connection contributions that come from the orbital angular momentum of the aggregate rotation of (the super clusters the make up the large scale structure of the ) the universe as whole.
In light of this we should reflect on the most appropriate kinematical objects and formalisms that should be deployed to describe such asymmetry.
Adding Structures to the Basic Manifold of Space
Einstein–Cartan, [EC] theory provides for an additional (through a space-time Torsional coupling) rotational (orbital and spin) degree of freedom as a metric but non-symmetric connection extension of the Einstein-Palatini (separate connection, verbein variable Variational) formalism of General Relativity.EC represents a minimal extension of GR from which one can encapsulate any violation of the cosmological isotropy principle through a rotating Universe. Once such bulk rotation on aggregate is plausibly identified one must find a means for capturing the universes' inherently orientable character. By enlarging the means by which space-time can be connected and thus its set of invariance preserving co-ordinate transformations, spin and orbital angular momenta contributions from matter can be coupled to the asymmetric ("axial") torsion connection components resulting from a minimally extended Variational Principle.
Orbital Angular Momentum is a Poincare (Lorentzian cross translational) invariant in the purely kinematical arena of Special Relativity in which no dynamics is afforded to its inert (literally!) spatial substrate. Angular momentum is the archetypal pseudo vector as described by axb below.
 In the matter encapsulating, more corporeal accepting General Relativistic dynamical arena it only retains a pseudo-tensorial (density) status. Space-time's malleability in the presence of matter (adhering to either Bose or more pertinently here Fermi statistics) invites orient-ability as well as the curvedness embodied in its holonomy. How do we build on the abstract notion of a rubber sheet manifold?
In the matter encapsulating, more corporeal accepting General Relativistic dynamical arena it only retains a pseudo-tensorial (density) status. Space-time's malleability in the presence of matter (adhering to either Bose or more pertinently here Fermi statistics) invites orient-ability as well as the curvedness embodied in its holonomy. How do we build on the abstract notion of a rubber sheet manifold?We look to add minimal set of structures to our abstract descriptive space:
https://www.mathphysicsbook.com/mathematics/topological-spaces/generalizing-surfaces/summary/
By adding metric structure lengths can be measured and compared at different points in the space if the space does not possess any strange shearing structures. Kinematically the most natural objects to represent spinning matter's frame dragging effects are two spinor-differential (multivector)-forms. Just as half-spin matter fields are most naturally modelled as invariants under the Special Linear Group, (the double cover of the Lorentz group) source term, the tangent space of space-time also affords a natural two-spinor character.

Multivector Calculus
Roughly, while vector objects when parallel transported once around locally flat infinitesimal parallelogram circuits return with same orientation spinorial objects require two circuits in order to return with an identical configuration.
In the language of multi-vectors an orientated parallel-piped volume is equivalent to a pseudo-tensor density with a leading determinant of the space time metric term.
https://en.wikipedia.org/wiki/Multivector
We can see that the "2-blade", 2 forms as an anti-symmetric of one forms defines an orientation. These two planes can be treated as one of the variables in a Variational principle. That is, instead of the (metric/verbein) and connection form we use these bi-vectors as fundamental spatial elements.
Invoking liberally the language of quantum theory, in such schema the irreducible parts of fermionic matter and bosonic space-time both share a common spinor structure.
Pseudo-vectors such as the archetype angular momentum vector are most naturally described by the (Hodge) dual of a multi-form. This is because in the multi-vector formalism, the dual object is intrinsic to the space. That is, no higher-dimensional reference space need be invoked to encapsulate an otherwise extrinsically defined orientation-inducing action of identifying an axis of rotation.

Duality in the sense can operate on the locally flat tangent space indices (of the verbein) as well as on the generalised co-ordinate space.
Using the former Hodge "star" facilitates the construction of both self-dual Curvature (of the connection) objects and self-dual two-forms of orientated 2-spaces (of parallelograms, say). Lagrangians that deploy these most natural Chiral 2-forms are de-facto oriented formulations of gravity.
http://www.mdpi.com/1099-4300/14/5/958