A story here of the nature of numbers that descends into being a placeholder: an excuse to catalogue the Mapping types between categories of objects. By looking at the relation between the set of irrational numbers generated by the Riemann Zeta function and the pyramid ('Power Pascal triangle") series characterised by its Bernoulli coefficients we see an instance of a functorial relationship from Category theory.
The language used to describe some of our dearest ideas in mathematics seems overly onerous so I try here to traverse the foothills of category theory by sampling from the irrationals drawn from Bernoulli and Riemann Zeta "functional" series. The conclusion couched in the pseudo-arcania of Category theory is that modulo some coefficients pi^(2n) acts as "functor" relational mapping
between the Category of Riemann Irrationals, Xi and the Bernoulli Rationals, B.
Number types
the operations with fractions (Rationals, Q) that we would have first learned without reference to pairs of numbers, (p/q). The rules for the operations with sequences, that is, with Irrational numbers R, still belong to that [same] category of rules. Defining the Integers, Z as positive and negative Natural numbers with a zero.

Technically we have the following definition of two otherwise familiar algebraic structures:
- Monoid: the integers Z under multiplication (but with no inverses)
- Abelian group: the integers or real numbers under addition
The laws to the right are the basic operations we look for in sets of objects: that they remain "closed" under their operational influence.
Irrationals as sums of Infinite Series
An irrational (Real) number is but an infinite sequence of rational (reals). The archetype irrational number is that defined as the Riemann zeta function defined as an infinite sum of Real-(field)
valued rational, Q numbers:

Respecting summation order in Method of Differences
As an example of this respecting of ordering when manipulating series in order to determine their (finite) sum, consider the method of differences employed to determine the sum of the first 100 terms of the series 1/r(r+1):
If we want to determine the finite sum of
1/2+1/6+1/12+1/20+..1/100(100+1) =100/101,
we use the method of differences to cancel out subsequent terms.

For our purposes it is sufficient to note that the such (irrational) reals form an Abelian group under the addition + operation.
Similarly we can use this method to unpick the i=2:

"Power Pascale" pyramid formula by taking the difference of the left hand side of the i=3 formula and its (n-1)^3 equivalent.
Indeed the i=2 series can be written in terms of the Bernoulli numbers:
Whether or not the series is of rational 1/q (Riemann Zeta, Z) or polynomial (Bernoulli, B) form we talk of these numbers being irrational Real (-valued) fields. Indeed these are but an infinitely small subset of the set of irrational numbers.
Class of Algebraic structures (Object) set types
The operator types be they + or x define the Algebraic structure or "object type". Possible features of such structures are summarised (mathsphysicsBook) below.
- Semigroup but not monoid: the positive reals less than 1 under multiplication (no identity)
- Monoid but not group: the integers under multiplication (no inverses)
- Abelian group: the integers or real numbers under addition
- Ring but not integral domain: the ring of integers mod n for n not prime (zero divisor pq=n=0)
- Integral domain but not field: the integers (no multiplicative inverses)
- Field: the real numbers; the complex numbers

Morphism and Composition Mapping Types
A Functor can be thought of as a homomorphism (structure-preserving map between two algebraic structures of the same type) between two categories C and D; a mapping that- associates to each object in C an object- its image, f(X) in D,
- associates to each morphism in C a morphism preserving identity morphism and composition of morphisms
Within the algebraic structure of groups, rings, modules, etc. morphisms are usually (type preserving) homomorphisms.
The notions of automorphism, endomorphism, epimorphism, homeomorphism, isomorphism, and monomorphism all find use in describing relations between algebraic structures.
An object class consists of sets with a structure:
- in which morphisms would be mappings between these objects in which elements of one set X map one-to-many or many-to-one to a set Y of other elements
- the category would consist of both the class and the mappings.
Functor between Z and B
Now to set of sets and maps as we define a category :
- class of objects ob(C)
- a collection of sets of morphisms mor(X,Y) between these,
- morphism composition operator -"functor".
The set of Riemann Zeta Irrational functional objects, Z : map to the Bernoulli "polynomial" Rationals, B functions
map to the Bernoulli "polynomial" Rationals, B functions through the functor mapping:
through the functor mapping:
 .
.
 map to the Bernoulli "polynomial" Rationals, B functions
map to the Bernoulli "polynomial" Rationals, B functions
As such, the irrational pi^(2n) (modulo some coefficients) is the "functor" the relational mapping the Category of Riemann Irrationals to the Bernoulli Rationals.
Real valued Groups
We see below the functor mapping between Group Categorical object to Set and then to function Category the bottom most map of which defines the function in the Real Number field. Illustrations from mathsphysicsBook as:
Three Categories each with their closed sets of objects and mappings types are thus illustrated. While the morphisms operate within each category the functors make clearer their algebraic structural relations.

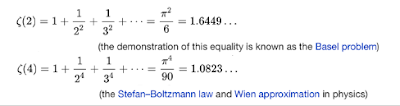






No comments:
Post a Comment