A Twisted Falling Frame Principle

From a metric to a falling frame field

All the insight that Einstein conjured from the off-shelf differential geometry of Riemann is captured in his Law of gravitation: that equating of the Ricci tensor to zero, . His assumption, that the contracted curvature in empty space is identically zero as the presence of only the gravitational field does not disturb the emptiness.

To see Newton’s theory as an effective field theory of Einstein’s vacuum equations, (1) note that the metric tensor,  are “potentials” for the gravitational field. There are ten Einstein metric potentials for just the one Newton-Poisson potential, . Like Newton the equating of Ricci curvature to zero delivers the usual second order (in ) field equation form, typical of physical laws.

Torsion of Space-rifling frames

“. . . imagine a space F which corresponds point by point with a Euclidean space E, the correspondence preserving distances. The difference between the two space is following: two orthogonal triads issuing from two points A and A’ infinitesimally nearby in F will be parallel when the corresponding triads in E may be deduced one from the other by a given helicoidal displacement (of right– handed sense, for example), having as its axis the line joining the origins. The straight lines in F thus correspond to the straight lines in E: They are geodesics. The space F thus defined admits a six parameter group of transformations; it would be our ordinary space as viewed by observers whose perceptions have been twisted. Mechanically, it corresponds to a medium having constant pressure and constant internal torque.” , Ellie Cartan, 1922

(i) A vector which is parallel transported along itself does not change, so a vector both directed and transported in x-direction.

(ii) A vector that is orthogonal to the direction of transport rotates with a prescribed constant ‘velocity” so a vector in y–direction transported in x–direction).

Even with flatness twistiness can exist.  With a metric connection with non-zero torsion vectors perpendicular to the tangent vector of a curve will rotate around it like a corkscrewing helix.

Crucially, Einstein’s potentials embodies both the gravitational field and the system of co-ordinates,  from which it is measured: unlike for Newton, Einstein’s field potential and the co-ordinate reference used to determine its components are inextricably mixed. This intertwining of co-ordinate axis and metric of interval measurement requires unpacking beyond the hackneyed image of the rubber-sheet inscribed with curvilinear co-ordinates. Indeed, in conjunction with his Weak (“Galilean”) Equivalence Principle, which asserts that test particles at alike spacetime points, in a given gravitational field, undergo the same acceleration, independent of all their properties (attributes, including their rest mass), in many ways the alternative bundle frame picture is preferable in describing the physics of the gravitational field. This weak EP is most famously tested and confirmed to great precision by the Eotvos experiment.

Accordingly the frame field on the tangent bundle, TM together with its dual co-frame field on the cotangent bundle, T*M over M is explored in the following.

Frame-verbein tetrad of fields

Given a metric tensor structure on a small enough locale of space,  the inner product of two vectors within ‘s tangent space can be computed directly. The tetrad (or verbein) field is that linear map from the tangent space to Minkowski space that preserves this inner product.

Frame fields,   are thus a set of four  orthonormal vector fields, one timelike,  and three space-like,  defined on a Lorentzian manifold whose integral curves are the world-lines of observers. An observed event on the worldline, is measured with respect to the triad of three space-like unit fields that define a local laboratory frame, L. The frame fields can be regarded as the “matrix square root” of the metric tensor as, 

Tensorial quantities defined on the manifold can be expressed either using the frame field,  on TM or its dual co-frame field, 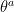 on T*M.

Soldering Functor as the Equivalence Principle

The stronger Einstein Equivalence Principle (EP)  further requires that the outcome of any local non-gravitational experiment in a freely falling laboratory is independent of the velocity of the laboratory and its location in spacetime. Einstein relativised accelerations not the velocities in the tangent space to 

Attaching a priori a Riemannian metric to  gives rise to a Cartan G-structure, (Orthogonal group) O(4) on it from which an holonomic co-frame bases,  can be defined for any non-holonomic co-ordinate bases,  identifies the functor  with the Pauli spin matrices when the G-structure group is   for which a symplectic metric,  on T*M imbues a spin()-structure on M determining a volume 4-form,  on it. 

Here we are using a holonomic basis for the group structure function in which .

A soldering of a fibre bundle to a smooth manifold is the attachment of fibres to the manifold in such a way that they can be regarded as tangent. Soldering expresses the idea that a manifold may have a point of contact with a geometry at each point. The frame bundle of a manifold M is a special type of principal bundle in the sense that its geometry is fundamentally tied to the geometry of M. This relationship can be expressed by means of a vector-valued 1-form on FM called variously the solder, fundamental or tautological 1-form.

The mathematical structures that embodies the EPs is the soldering functors,  labelled with spacetime, M coordinate,  and a local Lorentz-freely falling laboratory coordinate, . Local Lorentz indices are raised and lowered with the Lorentz metric, while general spacetime coordinates are raised and lowered with the metric tensor, .

Integrability of Connection

The non-integrability of parallel transport characterises the intrinsic notion of curvature of a space: as we parallel transport a vector u at p to q along two different paths vw and wv the resulting vectors at q differ by the measure of curvature of the space,  and the algebraic Bianchi identity is satisfied as in the diagram below.

If a theory is “gauge invariant” there should exist Bianchi identities analogous to those in Maxwell and Einstein’s theories which are identically satisfied. For Maxwell we have, by virtue of Stokes theorem that the electric current, J which enters the right hand side of the Maxwell equations  is conserved . The Bianchi identities as “integrability conditions” thus imply that the traceless divergence of the left–hand–side of equations of motion must vanish identically. This also implies that the currents of the matter fields if coupled to the gauge fields are conserved.

That a space maybe be teleparallel-flat but twisted is captured in the contorsion of the co-frame upon closed loop parallel transport.

Two vector fields u and v at point P.  Parallel transport u along v to become  and v along u to become . If a torsion is present, the lack of closure of this manoeuvre is a measure of the amount of spatial Torsion, (Hehl and Obukhov)

Whereas curvature is bivector-valued Torsion is vector-valued.