The field equations of a Metric theory can be derived from a first order Palatini formalism where an orthonormal frame 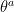 is used and in which the constraint that the dynamical connection is a metric compatible connection
is used and in which the constraint that the dynamical connection is a metric compatible connection  is put in by hand. The field equations read:
is put in by hand. The field equations read:
where the components of the energy-momentum,  and spin tensors,
and spin tensors,  are given in terms of the three forms
are given in terms of the three forms  ,
, 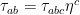 with
with 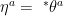 .
.
Here 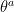 is an orthonormal “dual” (to tetrad) frame where indices
is an orthonormal “dual” (to tetrad) frame where indices 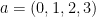 are Lorentzian time-space indices of a freely falling frame.
are Lorentzian time-space indices of a freely falling frame.
Kinematical differential Multivector framework
As Euler-Lagrange equations of a Lagrangian field theory, these Einstein-Cartan equations lend themselves to many alternative kinematical descriptions. Indeed they may be considered as a conservation law for a certain Sparling 3-form defined on the bundle of orthonormal frames over spacetime, 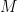 . They are most elegantly presented as two spinor-valued differential 3-form equations,
. They are most elegantly presented as two spinor-valued differential 3-form equations, 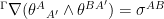
so that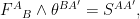 where
where 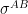 and
and 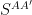 are known source quantities.
are known source quantities.
so that
For our purposes the main kinematical objects of a Variational principle are the 1-forms 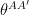 . These are the co-frame, verbein objects that are Einstein’s freely falling elevator. This dynamical variable,
. These are the co-frame, verbein objects that are Einstein’s freely falling elevator. This dynamical variable,  is a Hermitian matrix-valued one-form from which the (real Lorentzian) metric is given as
is a Hermitian matrix-valued one-form from which the (real Lorentzian) metric is given as 
For Real General Relativity the soldering functor is required to be real (
In constructing the 4-form Palatini Lagrangian we can make use of higher order multivector constructions based on the co-frame such as 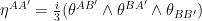
The internal indices  associated to the spin structure over space-time only acquires the interpretation as spinor indices through the dynamical soldering form,
associated to the spin structure over space-time only acquires the interpretation as spinor indices through the dynamical soldering form,  . A priori there is no relation between the tangent space and the internal space of the vector bundle
. A priori there is no relation between the tangent space and the internal space of the vector bundle 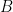 associated to the spinor structure over space time, M. Rather if a (non compact) spacetime manifold,
associated to the spinor structure over space time, M. Rather if a (non compact) spacetime manifold, 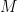 admits a global null tetrad it has a spinor-structure
admits a global null tetrad it has a spinor-structure  defined on it. A spinor structure,
defined on it. A spinor structure,  is a principal fibre bundle with structure group
is a principal fibre bundle with structure group 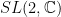 , the gauge group for spinor dyads. The (real) space-time manifold carries a
, the gauge group for spinor dyads. The (real) space-time manifold carries a 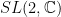 spin (trivial vector) bundle, B associated to
spin (trivial vector) bundle, B associated to  and its conjugate on it. The tensor product of these two bundles can be identified with the complexified tangent bundle. Each fibre,
and its conjugate on it. The tensor product of these two bundles can be identified with the complexified tangent bundle. Each fibre,  of B consists of a 2-complex dimensional vector space equipped with a symplectic metric,
of B consists of a 2-complex dimensional vector space equipped with a symplectic metric,  .
.
Cartan’s Structure Equations
With  and
and  (complex conjugate)
(complex conjugate)  -valued connection one-forms and the torsion two form denoted as
-valued connection one-forms and the torsion two form denoted as  , the first Cartan structure equation reads
, the first Cartan structure equation reads
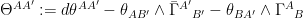
That is,
 where
where 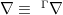 denotes the exterior covariant derivative with respect to the
denotes the exterior covariant derivative with respect to the  -valued connection(s).
-valued connection(s).
That is,
The internal `symplectic metric’,  is given as fixed so that the internal
is given as fixed so that the internal 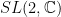 connection is then traceless
connection is then traceless 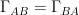 due to
due to 
Defining the basis of anti-self dual two-forms as

The second Cartan structure equations take the complex form
where the curvature two-form, 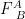 , has been decomposed into spinor fields of dimension 5,9,1 and 3 respectively , corresponding to the anti-self dual part of the Weyl conformal spinor,
, has been decomposed into spinor fields of dimension 5,9,1 and 3 respectively , corresponding to the anti-self dual part of the Weyl conformal spinor, 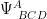 , the spinor representation of the trace-free part of the Ricci tensor,
, the spinor representation of the trace-free part of the Ricci tensor,  and the Ricci scalar
and the Ricci scalar  , – all with respect to the curvature of the
, – all with respect to the curvature of the 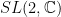 connection and
connection and  arising from the presence of non-zero torsion.
arising from the presence of non-zero torsion.
Here we have used the basis of anti-self dual two-forms  , defined in terms of the co-frame dynamical variable for mere ease of exposition. As we will see in a later post these objects can be treated as the bona fide, fully chiral dynamical “graviton” field object in tis own right.
, defined in terms of the co-frame dynamical variable for mere ease of exposition. As we will see in a later post these objects can be treated as the bona fide, fully chiral dynamical “graviton” field object in tis own right.
Semi-Chiral Lagrangian formulation Equations
Two Euler-Lagrange equations arise from Lagrangians of the general form
The internal  connection is not associated to the tangent bundle and is thus not a linear connection but a spinor connection. The variation of the Lagrangian with respect to
connection is not associated to the tangent bundle and is thus not a linear connection but a spinor connection. The variation of the Lagrangian with respect to  will determine this connection in terms of the co-frame so that the bundle
will determine this connection in terms of the co-frame so that the bundle 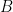 can then be considered soldered to
can then be considered soldered to 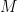 . The co-frame variation evaluated at the particular value of the connection just determined gives equations for the co-frames only. There exists a unique Levi Civita connection,
. The co-frame variation evaluated at the particular value of the connection just determined gives equations for the co-frames only. There exists a unique Levi Civita connection,  (with curvature
(with curvature 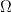 ) so the
) so the  connection,
connection,  can be decomposed according to
can be decomposed according to
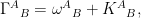
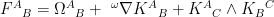
where is the contorsion one form, irreducibly written in terms of totally symmetric and`axial’ parts as
is the contorsion one form, irreducibly written in terms of totally symmetric and`axial’ parts as

The Einstein-Matter equations owing to the triviality of the Bianchi Identity

have the simpler form,
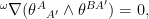
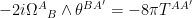
where
The Einstein-Matter equations owing to the triviality of the Bianchi Identity
have the simpler form,
It is possible to solve for  and replace any
and replace any  in
in 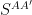 by
by  .
.
Semi-Chiral Lagrangian for Fermion fields
The Lagrangian for fermion matter has a dependence on the connection so admits torsion contributions but nevertheless can be written as the sum of a semi-chiral complex Lagrangian for vacuum General Relativity,  , a complex (semi)chiral fermion matter Lagrangian,
, a complex (semi)chiral fermion matter Lagrangian,  and a term,
and a term,  that ensures the standard Einstein-Weyl form of the field equations,
that ensures the standard Einstein-Weyl form of the field equations,
The 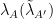 are the left (resp. right)-handed zero forms.
are the left (resp. right)-handed zero forms.
The theory uses only the anti-self dual connection, 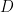 (which does not act on tensors, so for example
(which does not act on tensors, so for example
but is complete and it turns out, (by varying
Because ultimately the real theory is of interest (where 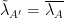 and
and  is hermitian) it proves useful to extend
is hermitian) it proves useful to extend 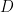 to
to  . Although it is argued that the spin
. Although it is argued that the spin 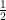 field variables can be taken to be either Grassman [or complex]-valued, in fact the use of complex spin
field variables can be taken to be either Grassman [or complex]-valued, in fact the use of complex spin 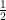 fields leads to a non-standard energy-momentum tensor which includes quartic spin
fields leads to a non-standard energy-momentum tensor which includes quartic spin 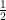 fields.
fields.
No comments:
Post a Comment