Our universe of apparently immutable Natural laws, appears to be well characterised by the sets of symmetries that can be viewed as generating them. In particular we observe a handedness choice of Nature more profound than that which differentiates our opposable thumbs. Notwithstanding the universe in aggregate being modelled pretty fairly at large enough scales as Isotropic with no preferred directionality to both its mass-energy content and the movement of that content, is Nature's "chiral" choice really any deeper than the necessity for an extended (non point-like "elementary") objects to have an orientation?
Symmetry and Chiral biases in Nature
An object is "chiral", possessing a handedness if it cannot be superimposed on its mirror image such that a Parity transformation would invert the object into its image.
In summarising the handed-orientability symmetry choices of Nature we will collate terminology from Chemistry, Physics and Mathematics and look at the algebra of the linear structures that underpin fundamental microphysics.
On a macroscale from Cosmology we see the signature of handedness in the polarised afterglow of gravitational waves embedded in the last scattering surface that is the Cosmic Microwave Background Radiation (CMBR). That we are built from left-handed amino acids begs a natural Anthropic question.
Lucky Linearity of Quantum Mechanics
Classically, the universe behaves in a weakly chaotic manner. All it's clockwork-like cyclicality is mostly illusory. The apparent simple periodicity observed in the universe belies a complex struggle between bifurcations of plausible orbits in the short term against the pull of long-term stability. That we have such stability at all in our rotating solar system is profoundly due to the fact that space is 3 dimensional. The multiplicity of words to describe Periodicity, cyclicality and orbits trace a tribute to some simple governing inverse square law, but some precession of the orbits point elude to this uneasy state of equilibrium.

That chaos is just a small perturbation away is due to the non-linearity of the gravitational field equations describing the systems' trajectories: a system of interacting particles given a little kick (perturbation) by the addition of another small body, will behave in a manner that will embody more than the sum of these two parts: it's behaviour will not be deterministic (
independent). .
The simplicity of Linearity is present in a system comprising the addition of a static electric charge (electron) to a set of other static charges. Applying the (apparently) natural Superposition principle gives the resultant Coulomb force on each particle as
being equal to just the net linear sum of all the Coulomb forces of the other charges. See diagram aside (
dmr-physicsnotes.blogspot).
In the quantum description Superposition conjures up multi-paths of a particle (-wave) appearing, as in a many-worlds manner, to coherently follow as it passes between two slits all available paths to a screen in the classical interferometer experiment.
Happily for those seeking to reduce our patterned but ultimately turbulent world to a mechanics of primitive basic building blocks these simple rules of linearity preside over the quantum realms of the very small. The mechanics of the quantum, be the fundamental root element of point-like, string-like or brane-like form, is linear in nature.
That is, the possible states of a physical object at its most basic level form a linear space that are eloquently described by Sophius Lie's (continuous) Group theory.
Thus these laws can be systematically applied to the electron cloud orbital shell systems around an atom's nucleus. The supreme reductionists have revealed the theory of linear representations of Lie algebras as underpinning fundamental symmetries of their universal primitives. Those entities composed of no other sub-entities, as Prime numbers: those non composite numbers with no simpler roots. A little discouragingly for believers in the reductionist programs (over dynamical system theorists) we know that just as the Prime numbers are infinite in number so are the number of coherent String theories that look to extend the primitive from a point to a wiggle.
Spin Sensitivity of Matter
In Quantum (Linear) Mechanics, operators give rise to the observables (vector) states that we see as the s and p shell eigenvalues of an atom. Such Linear Operators mark out the energies of the atom's states. The nuclei of such atoms themselves possess dipole moments, in which their Angular momentum, J preccess in an external magnetic field akin to a gyroscope immersed a torque inducing "gravitational" field.
The gyromagnetic ratio equal to  is the proportionality constant relating the "Larmor" frequency of this precession to that external magnetic field, B. In nuclear physics the g is a composite of the nucleon spins, their orbital angular momenta, and their couplings. As such spinning, be it intrinsically a "point" elementary particle (like an electron) or a composite nuclei marks out an orientation for aggregated matter. That most aggregated matter is charge neutral but not inertial mass neutral means that though it may not precess in any ambient magnetic fields it will exhibit De-Sitter (geodetic) and Lense-Thirring precession by virtue of being in the presence of a static (resp. rotating) central larger massive body.
is the proportionality constant relating the "Larmor" frequency of this precession to that external magnetic field, B. In nuclear physics the g is a composite of the nucleon spins, their orbital angular momenta, and their couplings. As such spinning, be it intrinsically a "point" elementary particle (like an electron) or a composite nuclei marks out an orientation for aggregated matter. That most aggregated matter is charge neutral but not inertial mass neutral means that though it may not precess in any ambient magnetic fields it will exhibit De-Sitter (geodetic) and Lense-Thirring precession by virtue of being in the presence of a static (resp. rotating) central larger massive body.
Left-handed -amino acids
We describe a “chiral" molecule as one that possesses a handedness in the sense that it is not superimposable with its mirror image.
So, just as left and right hands have thumb and fingers in the same order are mirror images but (arguably functionally) not the same, chiral molecules are molecule pairs that have the same atoms attached in a complimentary configuration, but which are mirror images and thus, not deemed identical.
Although most amino acids can be synthetically produced in both left and right-handed forms, left-handed amino acids almost exclusively dominates the life forms of Earth. It has been shown that some of the amino acids that fall to earth from space are more left than right handed prompted the search for such Chirality on the recent Rosetta-RSA mission to comet 67P/C-G.
Most DNA double helices are right-handed.
That is, if you were to hold your right hand out, with your thumb pointed up and your fingers curled around your thumb, your thumb would represent the axis of the helix and your fingers would represent the sugar-phosphate backbone. Only one type of DNA, called Z-DNA, is left-handed. Formation of this structure is generally unfavourable, although certain conditions can promote it.
A crude evolutionary analogy serves to indicate why a dominant configuration has prevailed. Consider the choice of handedness of the spiral staircases in medieval castles that served best as a means to defend. They were (almost) always built with the spiral going in the same direction according to the right hand screw rule as one looks down the stairs from above so that the defending right- handed swordsman, who would either be coming down the stairs or backing up in reverse, could freely swing his sword.
The attacking swordsman (ascending the stairs), unless left-handed would have his swing blocked by the wall. (
cmrp blog)
As such only a army of left-handed soldiers will have parity in the battle. Of course if they happen to succeed they will be at a disadvantage in defending the castle against another horde of lefties and be afforded no advantage over subsequent right-handed foes.
Polarization of electromagnetic fields
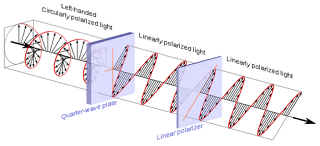
An ordinary incandescent bulb (just like the Sun’s radiation) emits (many wave packets of) photons pointing in random directions so its radiation is not said to be Polarised in any one direction. The propagating electromagnetic wave comprises intertwining electric and magnetic fields. By definition a wave's direction of polarization is defined to be the direction in which its electric field is oscillating. We can have linearly polarised, elliptical and circularly polarised waves.
While looking at the source, if the vector of the electric field part of the light coming toward you appears to be rotating counterclockwise then the light is said to be right-circularly polarized. Using such a wave description, the electric field vector and its intertwining magnetic field vector of circularly polarized (
wikipedia) radiation describe a helix.

As with all field equations those of Maxwell's varying electromagnetic fields are invariant to the reversal of time: change t to - t and they still work. (This is in contrast to what we know from his Thermodynamics where the arrow of time points only in the direction of increasing Entropy, to a universe sinking to a final equilibrium state of zero useful working energy). The helix is palindromic in time in the sense that the horizontally oriented helix is identical whether traversed into or out of the page in the diagram above: a reversal merely inverts the direction of the propagation of the light and does not modify the sign of the helicity. By convention though we define left handed helicity by the motion of the Helicity vector scribing the tip of the hands of a standard clock as it moves with the light ray with its face directed forwards.
Light-Handedness?
Does this choice of helicity reflect a real certain intrinsic handedness present in the light? Unlike the inversion of time there is a real effect of inverting the sign of spatial directions on the description of the light ray. Such an inversion operation is called a Parity transformation. It turns out that the study of such orientation dependence has had deep influence in the building of fundamental particle theories. The inversion of space transforms right-circularly polarized radiation into left-circularly polarized radiation. As such the helicity of radiation flips sign with a parity transformation and thus we can assert that circularly polarized radiation possesses a handedness called
chirality. The Quantum field theory take on the distinction between helicity and chirality is a little more subtle and was discussed in
from-chirality-to-helicity Whereas helicity (meaning "twisted")
is defined via the direction of the momentum and angular momentum of a particle it is not a Lorentz-invariant property for massive particles. In the massless case of light photons, helicity is synonymous with chirality as you cannot attach an inertial frame to a photon to observe it moving in a relative manner.
Optical Rotation
When linearly polarised radiation (say that has scattered off the plasma at Baryogenesis) traverses a medium that is "chiral" in the sense that it is filled with handed "enantiomer" molecules, one of the circularly polarized components is propagated less rapidly than the other and the plane of the polarized light beam becomes rotated. This phenomenon is called optical rotation (
chemgapedia).

If the beam is traversing a medium that is chromophoric, one of the two circularly polarized components is absorbed more than the other resulting in the phenomenon of circular dichroism.
Uneven-handed questions

The question you might ask then is why is there an apparent handedness choice present in the chiral compounds that gave rise to the life that observes this universe. In particular, why is it that almost exclusively there are only left handed amino acids within life on earth?
Is this due to some handedness in the radiation signature that was emitted at the Big Bang?
More precisely (
harvard.edu) does the light emitted from the surface of last scattering with its circularly polarized signature (a.k.a the Cosmic Microwave Background Radiation, CMBR) reflect some very early choice that has been made in the subsequent ert life that would come to exist in it. As the fireflies drawn to the light are we not drawn to the inescapable conclusion that our chiral flesh was cast from the tumult of circular polarised waves, the primordial evolutionary filter, the progeny of left-fit enantiomers.














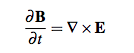

















 is the proportionality constant relating the "Larmor" frequency of this precession to that external magnetic field, B. I
is the proportionality constant relating the "Larmor" frequency of this precession to that external magnetic field, B. I