Maxwell's field equations governing the "Classical" electromagnetic field are described as "Linear". In the following we describe this quality through its vector calculus and differential form formulations. We note some expressions of apparent non-linearity in the electromagnetic field as suggested by the quantized version of its field theory. As such the following questions are addressed:
- What makes intertwining Electric, E and Magnetic, B fields in some sense a linear wave yet have possess a non-linear character?
- How is handedness characterised in complex "Dual" formulations of Maxwell equations?
- What does Ahranov-Bohm have to say about the linearity of intertwined E and B phenomena?
- How is is that QED says that light-light interactions are possible?
Linear in Maxwell's Field equations
The principle of superposition applies to electromagnetic field described by Maxwell's equations given they are linear in both the sources and the fields. So if you have two solutions to Maxwell's equations for two separate sources then the sum of those two solutions will be the same solution as if you just added together the two sets of sources. Such linear superposition is in contrast to non-linear interacting water-soliton or gravitational waves in which as in case of water waves, surface tension and frictional forces between layers create positive feedback loops. The formation of cross wave soliton being an example of the sum of two waves being more than the sum of their parts. Such are the complexities of the fluid dynamics as described by non-linear Navier-Stokes equations. Light at least before it scatters is trite in comparison.
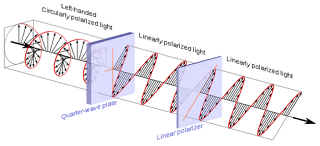
So for example, linearised polarisation of light arises out of non polarised light scattering off the flat interface of the air and water. Due to linearity, such linearised polarized radiation can be described as a combination of right-circularly and left-circularly polarized radiation, a form of Fourier decomposition of the wave.The equations describing the interaction of light with charged matter, their gauge freedom and linearity as captured in Maxwell's equations are briefly summarised in the following.
Magnetic monopoles unlike electric charges (as described by Gauss' law) do not exist:
Such Dipole generated fields, B are divergence free because they may be written in terms of the curl of a gauge potential, A
that in themselves are defined uniquely only up to addition of an gradient of a scalar field. Faraday's law describes how that changing magnetic field, B gives rise to a curling Electric field,
In a tensor formulation we form a four-vector A=(V, A) (𝜇=0,1,2,3) for (x,y,z=1,2,3) that is defined modulo a gauge ("phase") transformation:
A circle as the locus of points scribed by a radial vector of length, r can be described by radial (polar) co-ordinates (r, φ). Here φ is both angle defining a complex number on the unit circle and the phase of a sinusoidal function.
It is these very trigonometric (sinusoidal) functions of Ptolemy's astronomy that are the (eigen) function (complex exponentials) invariants with respect to time translation. An experiment’s results should not depend on the day they were made and the sine function is as homogenous as they come. As such they are the appropriate functions for linear systems. Indeed they are more than time translation invariant being palindromic as well. Quantum states being absolutely additive have such trigonometric functions as their eigenfunctions.
The Electric, E and Magnetic fields, B can be encapsulated as
which suggests an antisymmetric matrix form:
Ampere's law which through symmetry requires the introduction of time change displacement "current" field for charge and current densities can be written as
that is,
In order for this set of equations to be captured in Lorentz invariant matrix form a (Hodge) dual ★ "metric structure" needs to be added to our space. That is using the Levi-Cevita like symbol defining an orientation we have the object ★F
The multivector form of Maxwell's equations then takes the extremely compact form of a Bianchi identity and a source equations that makes their linearity apparent:
The differential form operator d when applied twice to a Field, F delivers zero. The main takeaway, mathematics aside is that the electromagnetic field is F=dA is the physical, observable field and that A the field potential, as merely an equivalence set is not physically realisable.
The proceeding field theoretic formulation is called a non-chiral (i.e. Parity symmetric preserving), "vector" (as in gauge boson) theory. The familiar "vectors" of three-dimensional space are the objective-invariants -staying the same when the underlying basis (co-ordinate axis) set is rotated. This vector quality of a mathematical object renders it as a realisable "observable" in nature.
A purely chiral formulation of Maxwell's equation can be made by forming the complex valued ant-self dual object, F-i★F.
The Relativity of Helicity
In the quantised field versions of classical field theories massless gauge vector bosons have spins that are in the same direction along their axis of motion regardless of the point of view of the observer. That their Chirality is absolute in this sense is due to both the invariance and finite speed of light. That such massless particles move at the speed of light, means that a massive observer (travelling at less than the speed of light) cannot travel in a faster reference frame in which the particle would appear to reverse its relative direction.
The photon's handedness is unambiguous in that all real observers see the same chirality. Accordingly we say that the direction of spin of the massless particles is not affected by a Lorentz boost (the relativistic equivalent of a Galilean change of reference frame) in the direction of motion of the particle. As such the sign of the projection (helicity) is fixed for all reference frames.
A photon’s “twistedness” has a sense in that helix described the rotation of its electric field (say) can be clockwise or anti-clockwise. By definition the helicity of a particle is right-handed if the direction of its spin is the same as the direction of its motion. It is left-handed if the directions of spin and motion are opposite.
Aharanov-Bohm Double Slit experiment
 In the double slit experiment we observe an interference pattern based on the superposition of waves arriving on screen in phase but travelling different path lengths be the missile a set of (or indeed single) electron(s) or (coherent set) of photon(s).
In the double slit experiment we observe an interference pattern based on the superposition of waves arriving on screen in phase but travelling different path lengths be the missile a set of (or indeed single) electron(s) or (coherent set) of photon(s).The Aharonov–Bohm effect is the shift in the interference pattern of a quantum mechanical double-slit experiment in which a magnetic flux carrying solenoid is placed between the two slits in the barrier. The phase, α, of the wave-function of the electrons going through each of the slits and onto the screen are phase shifted thus translating the interference pattern.
The effect shows the physical nature of the vector potential, A which is classically otherwise deemed the convenient mathematical ("Gauge Theoretic") artifice described previously.
The electrons move in a region, outside the solenoid where the magnetic field strength B=∇xA is zero. This means there is no Lorenz force acting on the electrons. The gradient of the field potential, A however just falls off as 1/r from solenoid. The A as discussed is gauge variant (ambiguously defined up to the addition of a gauge transformation of the derivative of scalar potential, V). The resulting phase difference however is gauge independent since it can be turned into a (gauge invariant) surface integral of the magnetic field. A variant invoking Faraday's law is the following scenario.
A cylinder, with a wire along its axis, takes the place of the solenoid.
The wire is fixed in space and the cylinder is free to rotate about it. The wire and cylinder carry equal and opposite charges, distributed uniformly; outside the cylinder their electric fields cancel, and once again the electron feels no electric force.
The cylinder, if it rotates, produces a magnetic field that vanishes outside it (like the magnetic field of a solenoid). So the electron also feels no magnetic force.
However, the electron acts upon the cylinder: the passing electron generates a magnetic field, and the changing magnetic flux through the cylinder induces an electric field curling around it (by Faraday’s law). This electric field changes the angular speed of the cylinder, but only briefly: the cylinder rotates freely with the same angular speed ω before and after the electron passes.
In all these scenarios the electric (electron) source's trajectory is guided by a gauge potential. the accumulated source of that potential thus does not dictate its motion. Linearity appears lost.
Laser-Laser Interactions
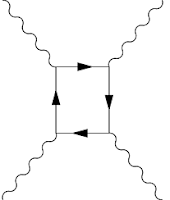
Light-by-light scattering is a quantum effect, whereby the two photons scatter from a virtual electron. Since this involves four photon-electron interactions, the process is heavily suppressed by a factor of roughly 1/137^4, making this process really rare (science mag).
Feynman rules of QED associate a factor -ie to each photon-electron-positron vertex, and there are four of those factors in the leading diagram (which is the "box diagram" with four such vertices).The fact that in QED there is no photon-photon scattering diagram with only two factors of -ie is the reason why photons do not scatter off each other as strongly as electrons.
In the classical picture an accelerating charge generates electromagnetic radiation. However, an accelerating mass generates no gravitational waves, which are only generated when the acceleration of the mass itself is changing. That is when the mass has a non zero “snap” (third order derivative of space”, to the fourth and fifth orders of “Crackle” and “pop”).
Gravitational waves if they are second quantizable would be carried by gravitons. A graviton is the excitation in the boson-gravitational field, travelling (according to 2017 results form binary-Neutron star coalescence to 15 orders of magnitude in precision to effectively ) the speed of light. It is a spin-2 particle, the only one, which means that it somehow needs only spin half a revolution before it arrives in the same position. Unlike a photon it is a source for the gravitational field itself. That is a graviton-graviton interaction. In this sense the graviton is non-linear (formed from a non-Abelian gauge theory) whereas the photon is not. The laser-laser interaction suggests otherwise at very high energies.



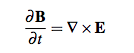










No comments:
Post a Comment