There are three quantitative number scales according to Psychologist Stanley Smith Stevens:
- Ordinal -rank ordering (1st, 2nd,..), sorting, Natural Counting numbers
- Ratio - mass, charge, Kelvin etc all with well defined origin
- Interval -Celsius, % change (first difference as fraction of original).
On a ratio scale the geometric mean (root mean square of an AC circuit) and the harmonic mean (Conductance of parallel electrical circuit) can be used to measure the central tendency in addition to the arithmetic mean which is all that is allowed on interval scales.
The Mathematical meaning of a Field
We do not live in Mathematical Asymptotia, dancing on the Euclidian plane, where pi actually is the ratio of the length of a circle to its diameter and the area under a hyperbola between the domain interval [0,1] is e. Only on Euler's complex plane are circles and waves united through e(), sin() and its poorer cousin sinh().
We live rather by (the rule of) laws not with them here in coarse-grain land. In a universe where length scale precisions ("least counts') of the latest gravitational wave interferometry experiments imply (equivalently) that we can discern to within the width (0.0.6mm) of a hair, the distance to Alpha Centauri 40 trillion km (wolfram calculator) away seems fine. That is within 10^-21m still 14 orders off the Plank length but still positively variegated in comparison to the continuity playground of Calculus. Whatever the coarseness of our view the measuring scale is a mathematical field.
With an origin, a ratio scale satisfies the rules of a division algebra, a ring (a set together with two binary operators +,*) in which every nonzero element has a multiplicative inverse, (where multiplication need not necessarily commutative).
A "field" is a commutative division algebra being a set of elements that satisfies the field axioms (table right-Wolfram) for both addition and multiplication. These are pretty much the rules you take for granted. It seems that nature doesn't always follow our intuition, dropping commutativity rules for Grassmann multivector calculus or spinor-quaternion fields and less pervasively admittedly associativity for Octonians. Complex numbers are the archetypal fields and we require that whether or not our formulations of physical theories are based on holomorphic functions with values enumerated in the the extended plane of Complex numbers we require "reality" conditions for the theories to be physical.
The character of change described by a physical dynamical field can be merely enumeration by way of a set of numbers (as for scalar Temperature) field or be (complex) tensor-valued as with gauge theories of the standard model of forces or gravitation that can be described by Complex-valued tensor or spinor fields.
The field assigns multiple numerical values of the same kind to multi-varied properties of extended parts of space-time. The concept enables variable changes in a quantity across space and or time. It is a means to encode related data as in temperature (scalar-valued) fields or pressure (co-vector- valued) isobars. For a scalar field the value of the field at each space point takes a scalar (numerical) value. The field captures an abstract ability to enumerate a continuous set of observations across space at any instant.
Faraday's field concept is though more than a useful means to describe the variation of quantities that characterise a phenomena. The Higgs field is such a scalar field that pervades all of space giving mass to quark excitations that interlace with them. Implicitly we have a means to carry or better have results relayed and gathered to us at some origin where we "measure" using our distribution of scaled rulers at all points in space. All such numbers enumerating a physical quality can then be usefully compared.
A "field" is a commutative division algebra being a set of elements that satisfies the field axioms (table right-Wolfram) for both addition and multiplication. These are pretty much the rules you take for granted. It seems that nature doesn't always follow our intuition, dropping commutativity rules for Grassmann multivector calculus or spinor-quaternion fields and less pervasively admittedly associativity for Octonians. Complex numbers are the archetypal fields and we require that whether or not our formulations of physical theories are based on holomorphic functions with values enumerated in the the extended plane of Complex numbers we require "reality" conditions for the theories to be physical.
The character of change described by a physical dynamical field can be merely enumeration by way of a set of numbers (as for scalar Temperature) field or be (complex) tensor-valued as with gauge theories of the standard model of forces or gravitation that can be described by Complex-valued tensor or spinor fields.
Playing the Faraday field.
The field assigns multiple numerical values of the same kind to multi-varied properties of extended parts of space-time. The concept enables variable changes in a quantity across space and or time. It is a means to encode related data as in temperature (scalar-valued) fields or pressure (co-vector- valued) isobars. For a scalar field the value of the field at each space point takes a scalar (numerical) value. The field captures an abstract ability to enumerate a continuous set of observations across space at any instant.
Faraday's field concept is though more than a useful means to describe the variation of quantities that characterise a phenomena. The Higgs field is such a scalar field that pervades all of space giving mass to quark excitations that interlace with them. Implicitly we have a means to carry or better have results relayed and gathered to us at some origin where we "measure" using our distribution of scaled rulers at all points in space. All such numbers enumerating a physical quality can then be usefully compared.
Natural Units of measurement
There are 4 primary SI units: three kinematical (meter, second, kilogram) and one electrical (Ampere). Regardless of the unit each maps to our idealised field-ratio scale.
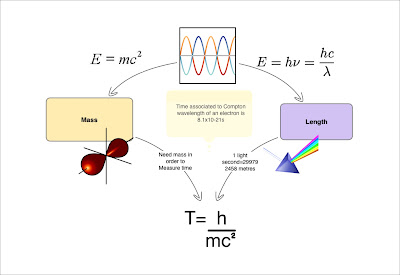
In fundamental physics we have a fundamental quantised unit for each of the Mass and Length scales. Time is deemed the most fundamental unit. From the picture on the right we can see se that without Mass in the universe we have no interval of time scale at all.
In the picture below we can see the fundamental nature played by time and the constant velocity of light in the vacuum. The latter defining length which is now deemed as derived from the notion of a velocity. The speed of light appears as an integer because the 'meter' has been redefined. All the kinematical units can be redefined in terms of the second (the 'duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom"). We then define the meter implicitly as the distance light in a vacuum travels given its speed of 299,792,458 metres per second. It is a change of precedence.
Temperature can be related to time by noting that of the Kelvin is thermodynamic measure of energy equal to the energy of a collection of photons whose frequencies sum to
135 639 274x10^-42 Hz.You can keep going defining the Kilogram and Kelvin as resp. the rest mass and thermodynamic measure of the energy of a collection of photons whose frequencies sum to 135 639 274x10^-42 Hz (see below)
For these measurement scales to be ratio scales given that all these measurements trace back to time requires a base origin time. Baryogenesis that delivered the asymmetry between mass and anti-matter in the universe some 300,000 years after the Big Bang delivers this in Standard models of Cosmology.
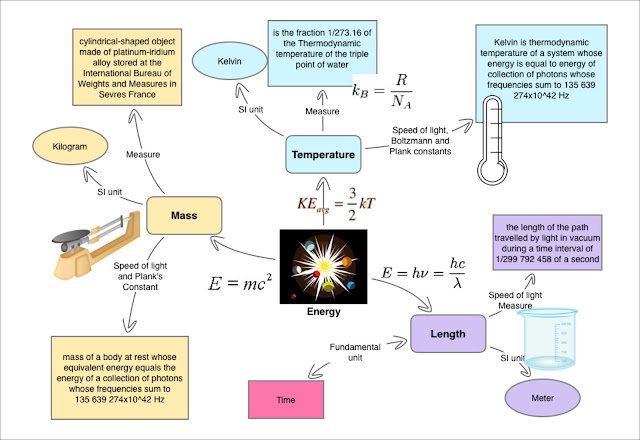
In fundamental physics we have a fundamental quantised unit for each of the Mass and Length scales. Time is deemed the most fundamental unit. From the picture on the right we can see se that without Mass in the universe we have no interval of time scale at all.
In the picture below we can see the fundamental nature played by time and the constant velocity of light in the vacuum. The latter defining length which is now deemed as derived from the notion of a velocity. The speed of light appears as an integer because the 'meter' has been redefined. All the kinematical units can be redefined in terms of the second (the 'duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom"). We then define the meter implicitly as the distance light in a vacuum travels given its speed of 299,792,458 metres per second. It is a change of precedence.
Temperature can be related to time by noting that of the Kelvin is thermodynamic measure of energy equal to the energy of a collection of photons whose frequencies sum to
135 639 274x10^-42 Hz.You can keep going defining the Kilogram and Kelvin as resp. the rest mass and thermodynamic measure of the energy of a collection of photons whose frequencies sum to 135 639 274x10^-42 Hz (see below)
For these measurement scales to be ratio scales given that all these measurements trace back to time requires a base origin time. Baryogenesis that delivered the asymmetry between mass and anti-matter in the universe some 300,000 years after the Big Bang delivers this in Standard models of Cosmology.
Dimensionless Structure Constants
Natural units in which speed of light and Planck’s constant become equal to one: c=1 and h=1 imposes two constraints on the three kinematical units leaving a free choice for one of the three kinematical units. The kinematical unit of the choice is energy, E, (measured in eV).(natural unit defined)
The fundamental bare elementary charge is electron, e 1.60217662 × 1019 Coulombs. All known elementary particles, including quarks, have charges that are integer multiples of 1/3 e. We say that the "quantum of charge" is 1/3e and "elementary charge" is three times as large as the "quantum of charge". The units of electric charge are defined by choosing the (empirically derived) permeability of free space to be ε0=1, which automatically sets μ0=1, since c^2=1/(ε0μ0). Since the units of force and distance in Natural Units are E^2 and 1/E, the electric charge is dimensionless in these units. Time does not need charge for it to create an ratio interval.
The expression of the fine-structure constant, as commonly found in older physics literature, is:
In natural units, where ε0 = c = ħ = 1, the fine-structure constant is That it is dimensionless is thus evident. Significantly then no man-made ratio-interval scale of which an alien race of beings would additionally need to be informed is required to share our ideas about the strength of interaction of electrons with photons.
No comments:
Post a Comment